在数学分析和复变函数中,级数的收敛性是一个重要的研究对象。尤其是在处理幂级数时,收敛半径的概念显得尤为关键。收敛半径不仅能帮助我们判定级数是否收敛,还可以为了解函数的性质和行为提供必要的信息。本文将详细介绍收敛半径的定义、计算方法及其重要性,并通过具体的例子来阐明这一概念。
一、收敛半径的定义
收敛半径(RadiusofConvergence)是指针对某一幂级数\(\sum_{n=0}^{\infty}a_n(x-c)^n\)的收敛区域,与中心\(c\)的距离。如果我们设该级数在\(|x-c|< R \) 区间内收敛,而在 \( |x - c| >R\)区间内发散,则收敛半径\(R\)就是这个\(R\)的值。值得注意的是,当收敛半径为零时,级数仅在\(x=c\)处收敛;而无穷大则意味着级数在所有\(x\)值下都收敛。收敛半径的大小直接影响到我们使用幂级数来表示复杂函数的能力。
二、收敛半径的计算方法
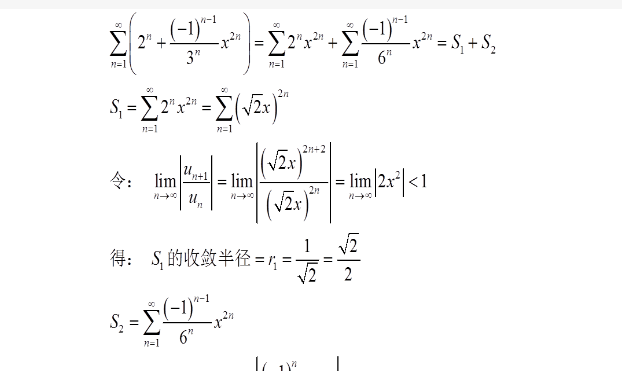
计算收敛半径的方法主要有两种:根式法和比值法。
2.1根式法
根式法是利用属级数系数\(a_n\)的\(n\)次方根来求收敛半径。具体公式如下:
\[
\frac{1}{R}=\limsup_{n\to\infty}\sqrt[n]{|a_n|}
\]
在这个公式中,\(\limsup\)表示上极限。如果我们能够计算出上述极限,就可以得到收敛半径\(R\)。
2.2比值法
比值法则是使用相邻系数之比来求解收敛半径。相应的公式为:
\[
\frac{1}{R}=\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|
\]
如果极限存在,便可以根据这个公式直接得到收敛半径。
这两种方法实际上是等价的,选择哪一种方法取决于具体情况。例如,对于一些特定形式的级数,某种方法可能更易于计算。
三、收敛半径的重要性
收敛半径在数学分析中的重要性体现在以下几个方面:
3.1函数近似
许多复杂函数可以通过幂级数来表示,例如指数函数、三角函数和对数函数等。在分析这些函数时,通过求得收敛半径,我们能够知道在哪些区间内我们可以安全地使用级数进行近似计算。
3.2数学分支的基础
在复变分析中,收敛半径是构建洛朗级数和傅里叶级数等复杂理论的基础。理解收敛半径能够帮助学生和研究者更深入地掌握复变函数的性质,从而进行更深层次的数学探讨。
3.3应用实际问题
在工程、物理等应用数学领域,许多问题可转化为幂级数形式求解。明确收敛半径能够指导我们选取合适的模型,从而提高解决问题的准确性和效率。
结论
收敛半径是数学分析中不可或缺的概念,它帮助我们判断幂级数的收敛性,并进一步应用于各种数学和工程问题的解决。通过根式法和比值法等方法,我们可以有效地计算出收敛半径,并在实践中加以应用。对于希望深入探索数学世界的学者及学生而言,掌握收敛半径的计算与应用意义重大。理解和运用这些工具,将有助于拓展我们的视野,提升解决问题的能力。
云作文原创内容,未经允许不得转载。