方差是统计学中经常使用的一种衡量数据分散程度的指标,它反映了一组数据的离散程度。对于方差越大还是越小越稳定的问题,我们需要根据具体的背景和应用场景来进行判断和分析。本文将从四个方面探讨方差的大小与稳定性的关系。
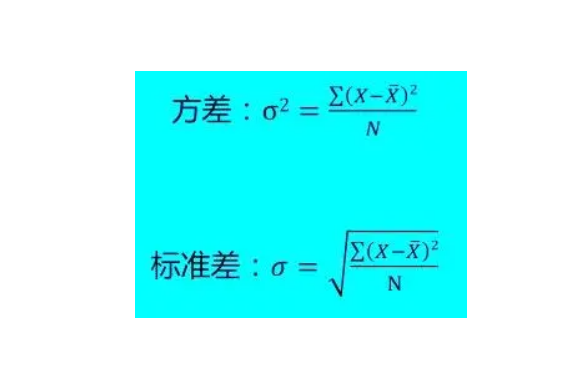
一. 方差越大越稳定的观点:
支持方差越大越稳定的观点主要集中在以下几个方面:1.方差的大幅度波动意味着数据的分布区间更广,这种情况下可能存在更多的机会和潜在的利润;2.方差大可以在某种程度上反映市场的不确定性和变化率,这对于投资者来说是一种稳定的状态,因为市场变化带来了更多的机会;最后,一些金融和投资模型则倾向于在波动较大的市场中寻找更多的收益机会,因此方差越大越稳定的观点在特定情况下是有理论依据的。
二. 方差越小越稳定的观点:
支持方差越小越稳定的观点主要集中在以下几个方面:1.方差小意味着数据分布更为集中,这种情况下可能更容易预测未来的趋势和走势,因而更加稳定;2.一些领域对数据的稳定性要求较高,例如工程设计、医疗诊断等,此时方差越小越能够保证结果的稳定性和可靠性;最后,一些金融人士和投资者可能更看重长期稳定的收益,因此会到较小方差的投资标的,从而获得更可预测和稳定的回报。
三. 方差与稳定性的平衡:
在实际应用中,我们需要权衡方差和稳定性之间的关系,到最合适的方案。在金融领域中,一般认为方差越小越稳定的观点更被广泛接受,因为投资者更倾向于稳定的收益和可控的风险。然而,对于创新型和高风险的领域,方差越大越稳定的观点则得到更多的支持。因此,在实践中,我们需要根据具体的背景、目标和偏好来平衡方差与稳定性的关系,选择合适的策略。
四. 方差稳定性的其他因素:
除了方差本身,还需考虑其他与稳定性相关的因素。例如,投资组合的多样性和弹性能够在一定程度上降低方差对稳定性的影响;市场发展水平和整体经济环境也会对方差的影响产生一定的调节作用。因此,在分析方差与稳定性关系时,需要综合考虑各种因素和要素,进行全面而深入的分析。
总结:
方差越大越稳定还是越小越稳定,没有唯一的答案。在不同的领域和应用情景下,不同的观点和判断都有其合理性。我们需要根据具体情况来选择最适合的方案。同时,方差稳定性的分析需要综合考虑其他因素,以得出更准确和可靠的结论。无论是支持方差越大越稳定的观点还是支持方差越小越稳定的观点,在实际应用中都需要以稳定性为前提,同时尽可能提高收益和降低风险,以实现更可持续和稳健的发展。
云作文原创内容,未经允许不得转载。