叉乘是向量运算中一种常见的运算方式,它用于求解两个向量的叉乘结果向量。在应用中,我们需要知道叉乘的方向是如何判断的。本文将详细讨论叉乘的方向判断方法。
一、什么是叉乘
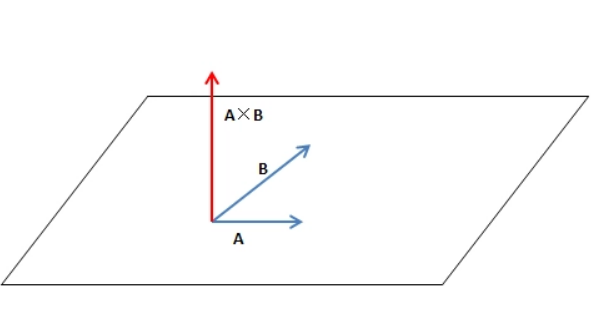
叉乘是向量运算中的一种运算方式,它的结果是一个新的向量。叉乘只适用于三维空间中的向量,其结果向量垂直于输入向量。
二、叉乘的定义
对于给定的两个向量a和b,叉乘运算的结果向量记为c。表示为c = a × b。叉乘运算的结果向量c满足以下两个条件:
1. c的模长等于a和b所构成的平行四边形的面积;
2. c与a、b都垂直,即c·a=0、c·b=0。
三、叉乘的方向判断方法
叉乘的方向判断可以通过右手定则来进行。右手定则规定了叉乘结果向量的方向。
1. 将右手伸直,让食指与向量a的方向一致,然后将中指与向量b的方向一致;
2. 使得食指与中指形成一个锐角(小于180°);
3. 转动手腕,让拇指的指向即为叉乘结果向量c的方向。
四、应用实例
下面通过一个应用实例具体说明叉乘的方向判断方法。
假设有两个向量a和b,向量a的坐标分量为(2, 3, -5),向量b的坐标分量为(-1, 4, 2)。
1. 求叉乘结果向量c的模长:
c的模长等于a和b所构成的平行四边形的面积。根据向量a和向量b构成的平行四边形的面积公式:
面积 = |a × b| = |a| × |b| × sinθ
其中,|a|和|b|分别表示向量a和向量b的模长,θ表示向量a和向量b之间的夹角。于是,可以得到:
面积 = |(2, 3, -5) × (-1, 4, 2)| = |(22, -9, 11)|
= √(222 + (-9)2 + 112) = √(484 + 81 + 121) = √(686) ≈ 26.19
2. 使用右手定则判断叉乘结果向量c的方向:
根据右手定则,将右手伸直,食指与向量a的方向一致,中指与向量b的方向一致,使得食指与中指形成一个锐角(小于180°),则拇指的指向即为叉乘结果向量c的方向。
3. 将向量a和向量b的坐标分量代入右手定则:
食指方向:向量a的方向,即向量(2, 3, -5)的方向。
中指方向:向量b的方向,即向量(-1, 4, 2)的方向。
转动手腕,拇指的指向即为叉乘结果向量c的方向。
综上,根据右手定则,叉乘结果向量c的方向为:(22, -9, 11)。
结论:
叉乘的方向可以通过右手定则来判断,根据向量a和向量b构成的平行四边形的面积,可以求得叉乘结果向量c的模长。叉乘在计算机图形学、力学等领域有广泛的应用,具有重要的意义。
云作文原创内容,未经允许不得转载。