在向量运算中,叉乘是一种常用的运算方法。通过对两个向量进行叉乘,可以得到一个新的向量,该向量的方向垂直于原来的两个向量。在实际应用中,往往需要判断叉乘向量的方向,本文将介绍如何通过右手定则来判断叉乘向量的方向。
一、右手定则的原理
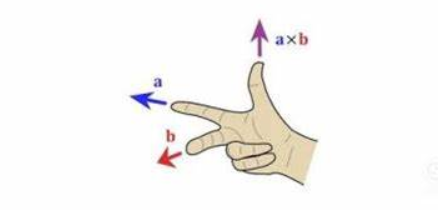
右手定则是在数学中用来判断向量叉乘的方向的一种定则。具体地说,右手定则是指:将右手的四指从向量a转向向量b,将四指弯曲成向量a到向量b的方向,那么大拇指所指的方向就是叉乘向量c的方向。
举个例子,假设有两个向量a和b,通过a和b的叉乘可以得到一个新的向量c,那么根据右手定则,将右手的四指从向量a转向向量b,四指所弯曲出来的方向就是c的方向。
二、实际应用
在实际应用中,我们需要根据叉乘向量的方向来进行一些判断。例如,在计算机图形学中,叉乘向量的方向可以用来判断一个三角形的法向量,从而实现光照效果。在机器人学中,叉乘向量的方向可以用来判断机器人手臂的运动方向,从而实现精准操作。
三、注意事项
在使用右手定则时,有一些需要注意的事项。首先,要保证右手的四指指向向量a和向量b的方向,否则得到的叉乘向量方向就会相反。其次,需要注意向量a和向量b的顺序,如果顺序颠倒,得到的叉乘向量方向也会相反。最后,需要注意向量a和向量b的夹角,如果夹角大于180度,则得到的叉乘向量方向也会相反。
结论:
通过右手定则可以判断叉乘向量的方向,这对于实际应用中的向量运算非常有用。在使用右手定则时,需要注意四指的指向、向量的顺序和夹角的大小,以保证得到正确的叉乘向量方向。
云作文原创内容,未经允许不得转载。