在三维几何学中,叉乘是一种常用的运算,它能够求出两个向量的垂直于它们所在平面的向量。然而,当我们进行叉乘运算时,如何判断其结果的方向呢?下面将为您详细介绍。
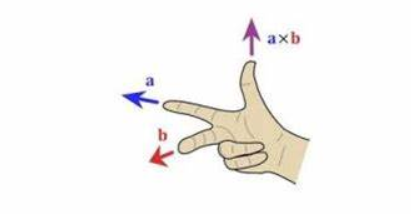
一、右手法则
判断叉乘方向的一种常用方法是右手法则。具体来说,我们可以将两个向量的起点对齐,然后将右手的食指指向第一个向量的终点,中指指向第二个向量的终点,然后用拇指指向垂直于这两个向量的向量所在的方向,此时拇指所指的方向就是叉乘向量的方向。
二、行列式法则
除了右手法则外,我们还可以使用行列式法则来判断叉乘向量的方向。具体来说,我们可以将两个向量的坐标表示为矩阵形式,然后将这两个矩阵按照行列式的形式进行展开,最后得到的行列式的符号就是叉乘向量的方向。如果行列式为正数,则叉乘向量方向垂直于两个向量所在平面向上;如果行列式为负数,则叉乘向量方向垂直于两个向量所在平面向下。
三、向量积分法
除了以上两种方法外,还可以使用向量积分法来判断叉乘向量的方向。具体来说,我们可以将叉乘向量表示为一个曲线的积分,然后使用斯托克斯定理将曲线积分转化为面积积分,最后得到的面积就是叉乘向量的大小,而面积的法向量方向就是叉乘向量的方向。
总结:
在三维几何学中,判断叉乘向量的方向有多种方法,其中右手法则、行列式法则和向量积分法都是比较常用的方法。通过这些方法,我们可以快速准确地求出叉乘向量的方向,并在实际应用中得到有效的应用。
云作文原创内容,未经允许不得转载。