向量叉乘是矢量运算中的一种重要方法,它可以求出两个向量所在平面的法向量,但在进行向量叉乘时,需要判断法向量的方向,下面就来介绍一下两个向量叉乘的方向判断方法。
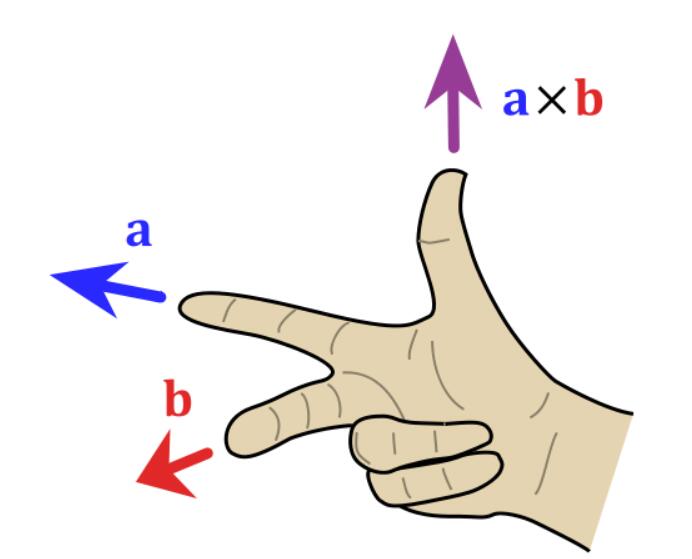
一、确定法向量方向的右手法则
向量叉乘的结果是一个新的向量,我们可以使用右手法则来判断这个向量的方向。如图所示,假设有两个向量a和b,将右手的四个手指指向a的方向,再将手腕向b的方向转动,拇指的方向就是法向量的方向。
右手法则非常简单易懂,但需要注意的是,如果a、b两个向量的顺序交换,那么法向量的方向也会相反。
二、使用行列式求解
向量叉乘的结果可以用行列式的形式表示,即:
```
a × b = | i j k |
|ax ay az|
|bx by bz|
```
其中i、j、k是三个互相垂直的单位向量,ax、ay、az和bx、by、bz是向量a和b的三个分量。
使用行列式求解向量叉乘,可以通过以下步骤确定法向量的方向:
1. 将向量a和向量b的三个分量分别写在第二、三行和第二、三列中。
2. 将第一行中的i、j、k依次与第二行和第三行的元素配对,每个配对中的两个元素相乘并带上正负号(具体方式见下文),然后将这些结果相加,得到法向量的x分量。
3. 同理,将第一行中的i、j、k依次与第三列中的元素配对,每个配对中的两个元素相乘并带上正负号,然后将这些结果相加,得到法向量的y分量。
4. 将第一行中的i、j、k依次与第二列中的元素配对,每个配对中的两个元素相乘并带上正负号,然后将这些结果相加,得到法向量的z分量。
在进行步骤2、3、4时,对于每个元素的正负号的确定,可以使用符号规律记忆法:
- 符号为正:从第一行的位置,顺时针旋转到第二个位置,再顺时针旋转到第三个位置,所经过的向量方向与向量a到向量b的夹角小于180度。
- 符号为负:从第一行的位置,逆时针旋转到第二个位置,再逆时针旋转到第三个位置,所经过的向量方向与向量a到向量b的夹角大于180度。
三、总结
使用右手法则和行列式求解都可以判断两个向量叉乘的结果的方向,不同的方法适用于不同的场景。在实际应用中,可以根据需要选择合适的方法,以便更加方便地求解问题。
云作文原创内容,未经允许不得转载。