在数学和物理领域中,叉乘是一种重要的运算方式。它不仅有着广泛的应用,还能帮助我们解决许多实际问题。本文将介绍叉乘的基本概念及其在确定方向上的应用,以便更好地理解和应用这一概念。
一:叉乘的定义和性质 叉乘,也称为向量积或叉积,是二维或三维空间中两个向量之间的一种运算。它的结果是一个新的向量,它垂直于原始两个向量,并遵循右手法则确定其方向。具体来说,对于给定的两个向量a和b,在三维空间中,叉乘的结果可以表示为向量c=(cx,cy,cz),其中: cx = aybz - azby cy = azbx - axbz cz = axby - aybx
叉乘具有以下性质:
叉乘的模长等于原始向量间的面积,并且它总是大于或等于零。
当两个向量平行时,叉乘的结果为零向量。
叉乘满足反交换律,即a×b=-(b×a)。
叉乘还满足分配律,即(a+b)×c=a×c+b×c。
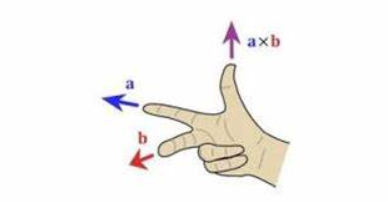
二:叉乘方向的确定 在使用叉乘时,我们经常需要确定结果向量的方向。为了做到这一点,我们可以运用右手法则。具体来说,将右手握紧,并使手指指向第一个向量a,并弯曲手指以指向第二个向量b。在这种情况下,大拇指所指的方向就是叉乘结果向量c的方向。这种方法可以帮助我们快速而准确地判断叉乘结果的方向。
三:叉乘方向判断的应用 叉乘方向判断在许多领域都有重要的应用,以下是其中几个例子:
物理学中的力矩:力矩是由力和力臂构成的。当两个向量之间存在叉乘关系时,根据叉乘结果的方向可以判断力矩的正负。这对于解决旋转、平衡和机械问题非常关键。
电磁学中的洛伦兹力:洛伦兹力的方向由电荷的速度、磁场的方向和两者之间的夹角共同决定。通过将速度和磁场表示为向量,并进行叉乘运算,可以确定洛伦兹力的方向。
计算机图形学中的三维旋转:在许多计算机图形学应用中,需要对对象进行三维旋转操作。通过将旋转轴表示为向量,并与待旋转的对象进行叉乘,可以获得新的旋转后的方向和位置。
总结: 叉乘是一种重要的运算方式,在数学和物理领域中有着广泛的应用。通过了解叉乘的定义、性质和使用右手法则确定方向的方法,我们可以更好地应用叉乘来解决问题。它在物理学、电磁学和计算机图形学等领域起到了至关重要的作用,帮助我们理解和描述各种现象和运动。
云作文原创内容,未经允许不得转载。