叉乘,也被称为向量积或叉积,是在向量代数中广泛使用的一种计算方法。它用于确定两个向量之间的关系,并为许多物理学问题提供解决方案。本文将向您介绍如何判断叉乘的方向。
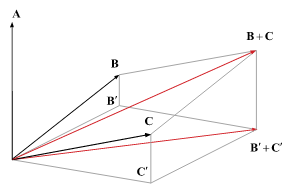
叉乘定义
在向量代数中,两个向量的叉积定义为:
A×B=|A||B|sinθn
其中,A和B是两个向量,θ是两个向量之间的夹角,|A|和|B|分别表示两个向量的大小,n是一个垂直于A和B方向的单位向量,其长度为1。
方向
叉积的方向可以由右手定则来确定。将您的手握成拳,让手指指向第一个向量的方向,然后将手腕旋转到第二个向量的方向。由于您的手是以第一个向量为基础的,所以您的拇指指向的方向就是叉积的方向。
例如,如果您将A向量放在您的指尖并弯曲手指以使它指向B向量,则您的拇指指向的方向是叉积的方向。您可以用相同的方法来找出B×A的方向,只需反转方向即可。
符号
叉积也具有符号,可用于确定其方向。如果两个向量的叉积的符号为正,则其方向与右手定则中描述的方向相同。如果两个向量的叉积的符号为负,则其方向与右手定则中描述的方向相反。
例如,如果A×B>0,则其方向与右手定则中描述的方向相同。如果A×B<0,则其方向与右手定则中描述的方向相反。
应用
叉乘可应用于很多物理学问题中。例如,在物理学中,叉积用于计算磁通量密度,永磁体电机的力矩,电荷某一点的力场及其导体磁力线的方向等。
结论
叉乘应用广泛且具有很多实际应用。判断叉积方向的标准是右手定则,其正负号可用于确定其方向。对于学习叉积的人来说,掌握这些基本知识非常有用,因为它们可以用于解决物理学和工程学中的许多问题。
云作文原创内容,未经允许不得转载。