在科学计算、数学建模和实验测量中,误差是不可避免的,绝对误差与相对误差的符号而绝对误差与相对误差的符号则是我们了解误差大小和方向的重要指标。在本文中,我们将深入了解绝对误差与相对误差的符号,以及它们对科学计算中的重要性。
1. 什么是绝对误差和相对误差?
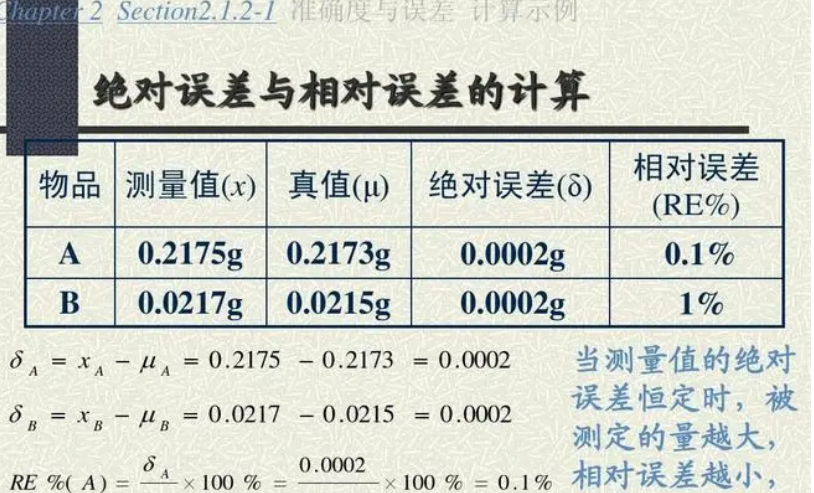
在科学计算和实验测量中,我们不可能完全得到精确的结果,因为存在各种原因会导致结果中的误差。而误差通常被分为绝对误差和相对误差两个部分。
绝对误差指数值近似值与准确值的差值,它反映了近似值离准确值的距离。相对误差则是绝对误差与准确值的比例,通常以百分数来表示,它反映了近似值相对于准确值的误差大小。
2. 绝对误差和相对误差的符号
在计算绝对误差和相对误差时,其符号对于我们判断近似值是偏大还是偏小至关重要。对于一个近似值a和准确值A,我们有以下结论:
– 当a > A时,绝对误差 Ea = a - A,相对误差 Er = Ea / A 都为正数。
– 当a < A时,绝对误差 Ea = A - a,相对误差 Er = Ea / A 都为正数。
– 当a ≈ A时,绝对误差 Ea ≈ 0,相对误差 Er 取决于测量精度,可以为正数或负数。
绝对误差与相对误差的符号告诉我们近似值偏离准确值的方向,如果我们不能确定近似值偏大还是偏小,就不能确定其误差的大小和方向。因此,我们在进行数学计算或实验测量时,应该保持谨慎,尽可能减小测量误差或计算误差。
3. 应用实例
下面是一些绝对误差和相对误差符号的应用实例:
– 在实验测量中,如果我们向上测量一个长度A,得到了一个近似值a1,向下测量同一长度A,得到了一个近似值a2,那么我们可以通过这两个数据计算出这个长度的平均值a = (a1 + a2) / 2,绝对误差Ea ≈ 0,相对误差Er = Ea / A < 1%。
– 在计算机学习中,经常需要使用代价函数来评估模型预测结果与真实结果之间的误差。如果代价函数为L,预测值为y,真实值为y ',则绝对误差Ea = L(y, y ')-L(y + h, y' )≈ h(dL / dy),相对误差Er = Ea / y ≈ h(dL / dy) / y。
– 在财务分析中,财务报表上的数据通常与实际情况相差较大,并且由于报表上的调整,可能会存在错误。因此,在财务分析中,要同时考虑绝对误差和相对误差,以便更好地了解企业的财务状况。
综上所述,绝对误差和相对误差是科学计算和实验测量中的重要指标之一,它们的符号可以帮助我们判断近似值是偏大还是偏小,以便更好地评估结果的精度和准确性。无论是在实验室、数学建模还是财务分析等领域,正确地计算并掌握误差符号的技巧都是非常重要的。
云作文原创内容,未经允许不得转载。