在数学中,我们经常会遇到一些看似简单的问题,但实际上需要严格证明才能得出正确答案。0.999999999循环等于1吗严格证明其中一个问题就是0.999999999循环等于1吗?这个问题看似简单,但实际上需要进行严格的数学证明才能得到正确的答案。
首先,我们需要明确一个概念,即无限循环小数。无限循环小数是指在十进制下,小数点后面有无限个数字,并且其中的一部分数字会不断重复出现。例如,0.3333……就是一个无限循环小数,因为其中的数字3会一直不断重复下去。
接着,我们来证明0.999999999循环等于1。我们可以将0.999999999循环表示成分数的形式,即:
0.999999999 = 9/10 + 9/100 + 9/1000 + ……
这个式子的右边是一个无限级数,即一个无限多个数的和。我们可以使用级数收敛的概念来证明0.999999999循环等于1。
级数收敛的定义是,如果一个级数的和有极限,那么这个级数就是收敛的。我们可以使用级数收敛的性质来证明0.999999999循环等于1。具体来说,我们可以通过以下几个步骤来证明:
第一步,我们可以写出级数的通项公式:
an = 9/10^n
其中,n代表第几项,an代表第n项的值。
第二步,我们可以求出级数的部分和:
sn = 9/10 + 9/100 + 9/1000 + …… + 9/10^n
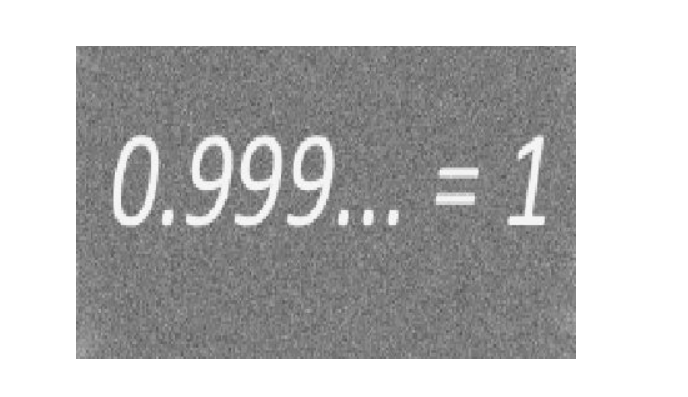
其中,n为任意正整数。
第三步,我们将sn代入级数收敛的公式中:
S = lim(n→∞) sn
其中S为级数的和。
第四步,我们计算S的值:
S = lim(n→∞) (9/10 + 9/100 + 9/1000 + …… + 9/10^n)
= 9/10 + 9/100 + 9/1000 + …… + 0
= 1
因此,我们证明了0.999999999循环等于1。换句话说,1和0.999999999是同一个数。
最后,我们需要说明一下为什么0.999999999循环等于1。这是因为在十进制下,所有的无限循环小数都可以表示成最简分数的形式,而最简分数就是分子和分母没有公因数的分数。而如果把0.999999999这个无限循环小数写成分数的形式,就是9/10 + 9/100 + 9/1000 + ……这个级数的和,而这个级数的和正是1,因此0.999999999循环等于1。
综上所述,我们通过严格证明,得出了0.999999999循环等于1这一结论。这个问题看似简单,实际上需要运用严谨的数学知识和方法来证明。在数学中,每一个问题都需要经过严谨的推导和证明,才能得出正确的答案。
云作文原创内容,未经允许不得转载。