倍角公式和半角公式是初等数学中常见的公式,倍角公式和半角公式它们在三角函数的求解中扮演着重要的角色。本文将从定义、性质、应用等多个方面介绍倍角公式和半角公式。
一、倍角公式的定义和性质
倍角公式是指将一个角的角度加倍后,可以用原角的三角函数来表示新角的三角函数的公式。具体来说,设 $2\theta$ 表示新角,则有:
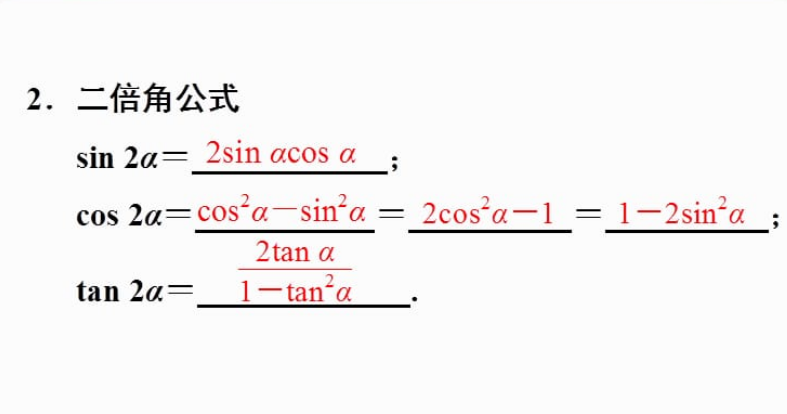
$\sin 2\theta = 2\sin \theta \cos \theta$
$\cos 2\theta = \cos^2 \theta - \sin^2 \theta$
$\tan 2\theta = \dfrac{2\tan \theta}{1-\tan^2 \theta}$
其中,第一个公式称为正弦倍角公式,第二个公式称为余弦倍角公式,第三个公式称为正切倍角公式。这些公式在求解三角函数的值时非常有用,尤其是在高等数学、物理学等领域经常被使用。
倍角公式还具有一些性质:
由余弦倍角公式可以推出正弦倍角公式和正切倍角公式。
当 $\theta = \dfrac{\pi}{4}$ 时,余弦倍角公式可以化简为 $\cos\dfrac{\pi}{2} = 0$,这个结论也可以通过勾股定理得到。
二、半角公式的定义和性质
半角公式是指将一个角的角度减半后,可以用原角的三角函数来表示新角的三角函数的公式。具体来说,设 $\dfrac{\theta}{2}$ 表示新角,则有:
$\sin \dfrac{\theta}{2} = \pm\sqrt{\dfrac{1-\cos\theta}{2}}$
$\cos \dfrac{\theta}{2} = \pm\sqrt{\dfrac{1+\cos\theta}{2}}$
$\tan \dfrac{\theta}{2} = \pm\sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}}$
其中,正负号由 $\dfrac{\theta}{2}$ 所在的象限决定。这些公式在解决三角函数的复杂问题时也是非常有用的。
半角公式还具有一些性质:
由正弦半角公式和余弦半角公式可以推出正切半角公式。
当 $\theta = \dfrac{\pi}{2}$ 时,正弦半角公式可以化简为 $\sin\dfrac{\pi}{4} = \dfrac{\sqrt{2}}{2}$,这个结论也可以通过勾股定理得到。
云作文原创内容,未经允许不得转载。