在现代数学和物理学中,向量作为表示具有大小和方向的量,扮演着举足轻重的角色。而在理解和处理向量时,维数这一概念显得尤为重要。向量的维数不仅决定了我们可以在多大空间中操作,还影响到数据的处理方式、计算的复杂性以及几何图形的表现形式。本文将深入探讨向量维数的含义,分类以及它在不同领域中的重要性。
一、向量维数的基本概念
向量维数可以简单理解为向量所在空间的“维度”。在数学上,维数是一个描述空间中自由度的量,它表示定义一个点所需的独立坐标数。对于一个n维向量空间来说,任何一个向量都可以用\(n\)个实数来唯一确定。
例如,在二维空间中,一个点的位置可以用两个坐标(如\(x,y\))来表示,这样的空间称为二维空间,而相应的向量就是二维向量。同理,在三维空间中,一点的坐标则需要三个数(如\(x,y,z\)),从而形成三维向量。因此,向量的维数正是描述其所处空间的维度,反映出该空间的复杂程度与层次结构。
二、向量维数的分类
根据不同的应用背景和实际需求,向量维数可以有多种分类方式。主要可以分为以下几类:
1.**有限维与无限维向量空间**
-**有限维向量空间**:这是一种维数是有限的向量空间,例如二维空间、三维空间等。在这些空间中,向量可以通过有限个基向量线性组合得到。
-**无限维向量空间**:相较于有限维空间,无限维空间的维数是没有界限的,比如函数空间。这样的空间中,向量(通常是函数)需要无限多个基函数才能完全描述。
2.**实数向量与复数向量**
-**实数向量**:这些向量的每个分量都是实数,广泛应用于工程、物理等领域。
-**复数向量**:其分量为复数,常用于量子物理和一些工程学应用。在复数向量中,向量的维数同样可以是有限或无限。
3.**线性独立与线性相关**
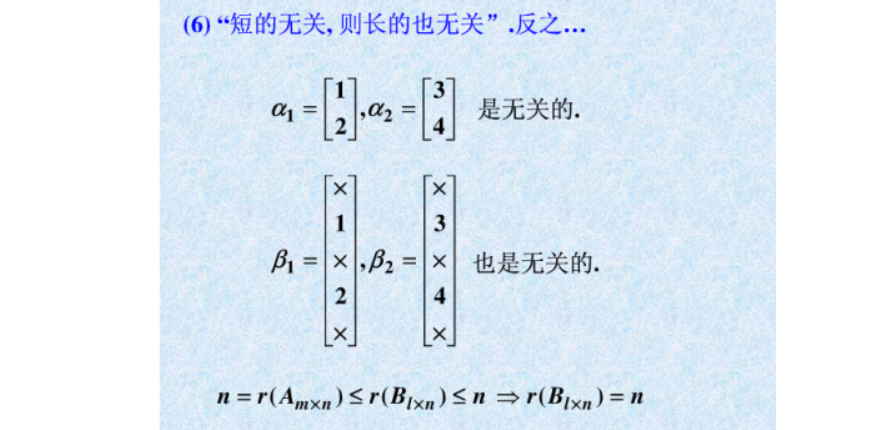
-**线性独立向量组**:一组向量如果无法通过其余向量的线性组合表示,那么这组向量就是线性独立的,其个数上限直接决定了这个向量空间的维数。
-**线性相关向量组**:若向量组中的某个向量可以由其他向量的线性组合表达,那么这组向量是线性相关的。相关向量的存在将会降低该向量组的有效维数。
三、向量维数的应用与重要性
向量维数在各种科学技术领域中均发挥着不可或缺的作用。
1.**机器学习与数据科学**
在机器学习中,数据集常常被表示成高维向量。数据的维数直接关系到模型的复杂度以及计算的高效性。理解维数的概念有助于选择合适的算法和模型,避免过拟合和欠拟合的问题。例如,PCA(主成分分析)是一种降维技术,其目的是通过减少特征的数量(降低维数)来提取数据中的主要特征。
2.**物理学**
在物理学中,许多现象都涉及到多维空间的概念。例如,描述一个粒子的运动状态可能需要考虑其位置的三维空间,加上速度、加速度等特征,形成一个更高维的状态空间。通过对向量维数的理解,物理学家能够构建更精确的理论模型。
3.**计算机图形学**
在计算机图形学中,物体的表示往往依赖于向量和其维数。三维建模中的每一个点在空间中的位置都可以用三维向量表示,而实现一些图像效果,如阴影和光照,则需要更多的维度来处理,从而使得图像更加真实。
结论
总的来说,向量维数是理解多维空间及其性质的基础,对于学术研究和实际应用均具有重要意义。从数学到物理,从计算机科学到工程技术,掌握向量维数的概念和应用将极大地提高我们的解决问题和创新能力。在未来的发展中,更深入和全面的理解向量维数也将为我们带来新的机遇与挑战。
云作文原创内容,未经允许不得转载。