在概率论和统计学中,“事件”是指某种特定的结果或情况,而“事件相互独立”则是一个重要的概念,它描述了两个或多个事件之间的关系。在日常生活中,我们经常会遇到许多事件,这些事件之间往往存在着一定的联系。然而,理解什么是相互独立的事件,对于科学研究、数据分析乃至日常决策都具有重要意义。本文将通过分段的形式,详细探讨事件相互独立的含义及其相关特性。
1.事件的基本概念
首先,我们需要理解什么是“事件”。在概率论中,事件通常被定义为样本空间中某个子集。举例来说,当我们进行一次抛掷硬币的实验时,可能出现的结果包括“正面朝上”和“反面朝上”,这两个结果分别可以看作是两个不同的事件。同样地,在复杂的实验中,事件可以是多个结果的组合。
2.相互独立事件的定义
事件相互独立的具体定义是:若事件A和事件B是相互独立的,则事件A发生的概率不受事件B是否发生的影响,反之亦然。用数学公式表示为:
\[P(A\capB)=P(A)\timesP(B)\]
这意味着,当你知道事件A已经发生时,事件B的发生概率仍然等于它自身的发生概率,而不会受到事件A的影响。
3.相互独立的例子
为了更好地理解相互独立性,我们来看一些简单的例子。假设我们有两个独立的随机试验:一个是掷骰子的结果,另一个是抛硬币的结果。无论掷出的骰子是几点(1到6),抛出硬币是正面还是反面,这两个事件之间没有任何依赖关系。这种情况下,掷骰子事件A和抛硬币事件B是相互独立的。
4.相互独立的条件
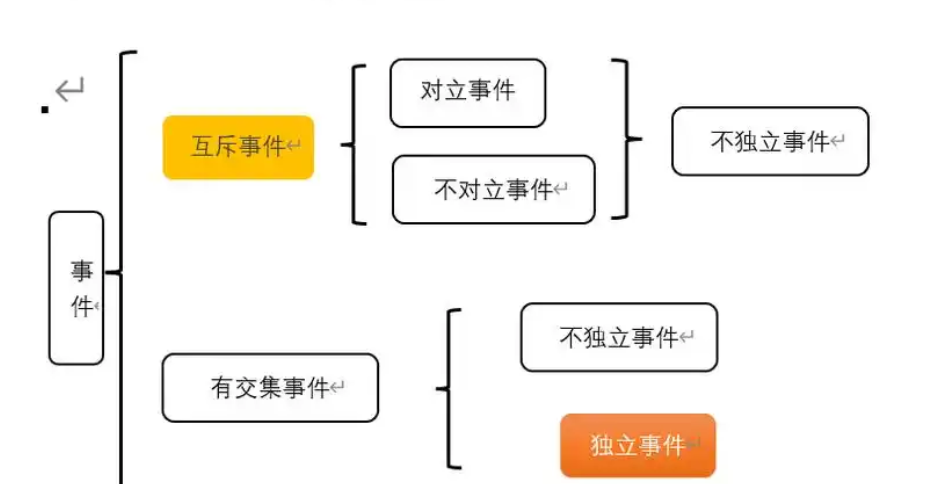
需要注意的是,不是所有的事件都是相互独立的。有时候,某些事件之间会存在关联性。例如,在一个班级中,如果学生A通过了数学考试,可能意味着其他学生通过考试的概率会有所变化。这种情况下,事件A(学生A通过考试)和事件B(其他学生通过考试)不是相互独立的。判断事件之间是否相互独立,通常需要比较它们的联合概率与各自的概率乘积是否相等。
5.相互独立在统计学中的应用
理解事件相互独立的性态在统计学中极为重要。例如,在进行假设检验时,研究人员必须确认样本数据是否满足独立性假设,以保证检验结果的有效性。在建模过程中,很多统计模型(如回归分析、方差分析等)都需要假设模型中的各个变量是相互独立的,否则可能导致错误的结论。
6.相互独立的误区
在实际应用中,人们经常会混淆“无关”和“相互独立”的概念。无关并不等同于相互独立,有些事件看似没有关联,但仍然可能彼此依赖。因此,在分析事件之间的关系时,需要小心谨慎,不能简单地假设它们是相互独立的。
7.实际生活中的相互独立
最后,相互独立的概念不仅限于数学和统计领域,在生活中也有很多实际应用。比如,在评估多个因素对某一结果的影响时,如果这些因素间是相互独立的,那么我们可以更加简单地进行加法或乘法运算来评估总体影响。这对于商业决策、风险管理等方面都十分重要。
结论
事件相互独立的概念在理解概率和统计模型中占据着核心地位。通过准确地识别和定义相互独立的事件,我们可以更加有效地进行数据分析和科学研究。在面对复杂的现实世界时,掌握这一概念能够帮助我们做出更加明智的决策。因此,了解事件相互独立,不仅是理论学习的要求,也是实际应用的重要基石。
云作文原创内容,未经允许不得转载。