双曲线焦点三角形是解析几何中一个有趣且复杂的结构。它涉及到双曲线的焦点、准线以及它们的几何关系。在这篇文章中,我们将深入探讨双曲线焦点三角形的定义、性质、几何特征及实际应用。
**一: 定义与基本要素**
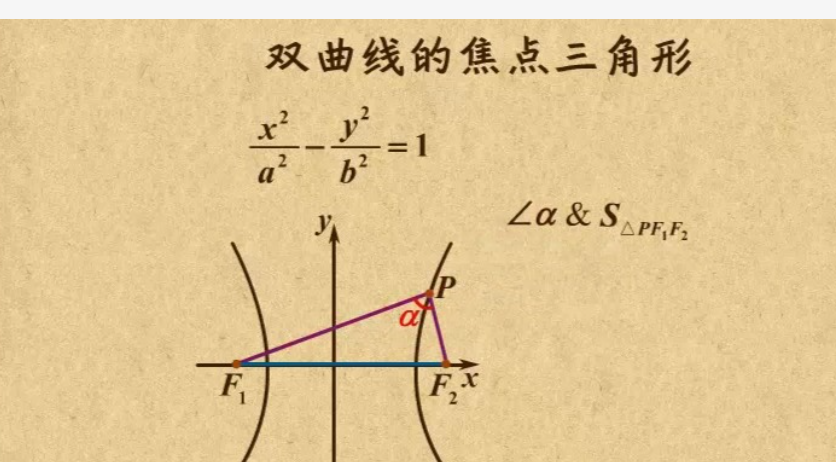
双曲线是一种二次曲线,其方程为$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$,其中$a$和$b$分别是双曲线的半实轴和半虚轴。双曲线有两个焦点,位于其中心(原点)的左右两侧,焦点到中心的距离$c$满足$c^2 = a^2 + b^2$。当我们连接双曲线的一个焦点与另一条支上的两个点时,我们形成了所谓的“焦点三角形”。
**二: 几何特性**
1. **直角特性**: 在双曲线上任取一点P和另一个焦点F',连接P到F和F',这个三角形PF'F永远是一个直角三角形,角在P处,因为双曲线的定义本身包含了点到两焦点的距离差等于常数的特性。
2. **等边三角形**: 如果选择的点在双曲线的矩形上(即$y=0$的水平线与双曲线交点),三角形恰好成等边形状,这是一个非常特殊的几何现象。
3. **面积关系**: 焦点三角形的面积可以用简单的公式计算,与焦距和选点的坐标有关,公式为:$Area = \frac{1}{2} \times F_1F_2 \times \sin(\alpha)$,其中$\alpha$是三角形的一个角。
**三: 焦点三角形的特殊性质**
- **焦点三角形的三个顶点总是位于同一条直线上**。这种现象可以借助双曲线的定比分点性质解释。
- **稳定性**: 无论在双曲线上选择什么样的点,焦点三角形的形状总是在某个特定角度范围内变化,这种稳定性为工程设计提供了理论基础。
**四: 实际应用**
1. **天文学**: 由于双曲线的轨迹常用于描述彗星的路径,天文学家在计算行星和彗星相对位置时常常利用这些几何关系。
2. **建筑设计**: 在一些现代建筑的外观设计中,双曲线的形态被用来打造流线型的外形,焦点三角形的性质可以帮助设计师确定结构上的特定点。
3. **射频工程**: 在无线电天线的设计中,尤其是反射式抛物面天线,双曲线的焦点三角形结构可以被利用来精确调节信号反射的路径。
**总结:**
双曲线焦点三角形不仅仅是几何中的一个美学点缀,更是因为其独特的性质在多个领域发挥着重要作用。从理论研究到实用设计,双曲线焦点三角形提供了一个理解空间关系的独特视角。通过本文对其定义、特性、性质和应用的全面介绍,希望读者能够对双曲线的这一方面有更深入的了解,并能够将其应用到实际问题中,激发新的创造力和技术突破。双曲线焦点三角形不仅是一项数学成就,更是科学与艺术交汇的完美例子。
云作文原创内容,未经允许不得转载。