$ln(x^2)$ 的导数为 $\frac{2}{x}$。
一、函数形式及基本概念
$ln(x^2)$ 是一个复合函数,其形式为$f(g(x))$,其中 $f(u) = ln(u)$,而 $g(x) = x^2$。复合函数的导数是通过链式法则计算得到的。
二、链式法则的应用
**链式法则**是求解复合函数导数的重要工具,其公式如下:
$$
\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)
$$
对于 $ln(x^2)$:
1. **外层函数** $f(u) = ln(u)$,其导数为 $f'(u) = \frac{1}{u}$。
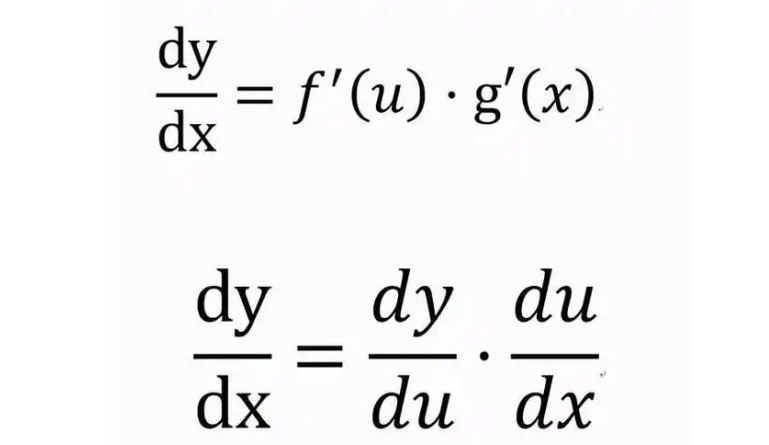
2. **内层函数** $g(x) = x^2$,其导数为 $g'(x) = 2x$。
应用链式法则:
$$
\frac{d}{dx}[ln(x^2)] = \frac{1}{x^2} \cdot 2x = \frac{2x}{x^2} = \frac{2}{x}
$$
三、分析与讨论
**1. 导数的意义**
导数 $\frac{2}{x}$ 表示在$x$点附近,$ln(x^2)$ 函数的切线斜率。如果我们考虑正负方向的问题:
- 当 $x > 0$ 时,导数是正的,表示函数在这一区间是增函数。
- 当 $x < 0$ 时,导数也是正的,表明函数在这段区间仍然是增函数,但需要注意 $x^2$ 是正数,因此其自然对数在负数区间也会保持一致性。
**2. 特殊情况**
值得注意的是,$ln(x^2)$ 在 $x=0$ 处是不连续的,因为对数函数的定义域不包括零,所以导数在这点不存在。
**3. 绘图解释**
如果我们画出函数 $y=ln(x^2)$ 和其导数 $\frac{2}{x}$ 的图像,可以发现:
- $ln(x^2)$ 在区间 $(0, +\infty)$ 和 $(-\infty, 0)$ 上是严格递增的,但由于对数函数的特性,其变化率逐步减小。
- $\frac{2}{x}$ 在正半轴是一个减函数,在负半轴是一个增函数,反映了$ln(x^2)$的变化速率随$x$的增大或减小而变化。
**4. 其他相关**
在数学和物理等领域,了解这类函数及其导数有重要的实际意义。例如,在信号处理、经济学中的增长模型,或者物理中的热传导问题中,这样的导数能够提供关于系统如何变化的信息。
总结
通过链式法则,我们得到了$ln(x^2)$ 的导数为 $\frac{2}{x}$。这个结果不仅验证了数学理论的正确性,也提供了一个具体的案例来理解复合函数的求导过程。这个知识对理解更复杂的函数,如对数函数的变形、双曲函数或复合三角函数等,有着显著的参考价值。
云作文原创内容,未经允许不得转载。