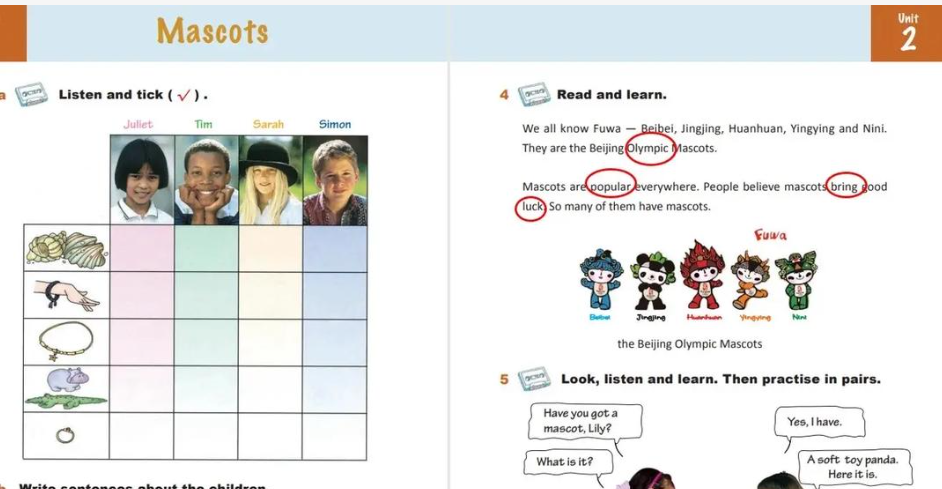
arcsinx的求导探究
导语
在微积分的世界中,导数是一项关键的工具,用来刻画函数的变化率。对于反三角函数来说,理解其导数不仅有助于深入学习微积分,还能在物理学、工程学等领域中发挥重要作用。本文将重点讨论反正弦函数 \( \arcsin(x) \) 的求导过程,帮助读者理解背后的原理及其应用。
反正弦函数的定义
反正弦函数 \( \arcsin(x) \) 是一个常见的反三角函数,用来表示与已知正弦值相对应的角度。具体来说,若 \( y = \arcsin(x) \),则 \( x = \sin(y) \),其中 \( y \) 的取值范围为 \( [-\frac{\pi}{2}, \frac{\pi}{2}] \);而 \( x \) 的取值范围为 \( [-1, 1] \)。
这一定义为后续的导数求解提供了基础。
导数的基本思想
在学习导数之前,我们先了解一下其基本思想。一个函数的导数在某一点的值,可以被理解为这个点处的切线斜率。用极限的语言来表述,即:
\[
f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}
\]
其中,\( f'(a) \) 就是函数 \( f(x) \) 在点 \( a \) 的导数。
使用隐函数求导法
要找到 \( \arcsin(x) \) 的导数,我们可以利用隐函数求导法。设定 \( y = \arcsin(x) \),那么我们有
\[
x = \sin(y)
\]
对上述方程两边同时对 \( x \) 求导,得到
\[
1 = \cos(y) \cdot \frac{dy}{dx}
\]
此时我们需要使用 \( \cos(y) \) 的表达式。根据三角恒等式,有:
\[
\cos(y) = \sqrt{1 - \sin^2(y)} = \sqrt{1 - x^2}
\]
因此,将 \( \cos(y) \) 带入之前的导数表达式:
\[
1 = \sqrt{1 - x^2} \cdot \frac{dy}{dx}
\]
求得导数表达式
接下来,解出 \( \frac{dy}{dx} \):
\[
\frac{dy}{dx} = \frac{1}{\sqrt{1 - x^2}}
\]
于是,我们得到了 \( y = \arcsin(x) \) 的导数:
\[
\frac{d}{dx} \arcsin(x) = \frac{1}{\sqrt{1 - x^2}}
\]
需要注意的是,这个导数的定义域为 \( x \in (-1, 1) \),当 \( x = -1 \) 或 \( x = 1 \) 时,导数是不存在的,因为在这两个端点处,反正弦函数的图像与 x轴的切线并不平行。
导数的几何意义
导数不仅是一个代数性质,它还有着深刻的几何意义。对于 \( \arcsin(x) \) 函数,其图像形状较为特征鲜明,整体呈现出如同拱形的走势。这一特征使得其导数在各个区间内均为正值,暗示函数在这些区间上是单调递增的。
通过绘制函数 \( y = \arcsin(x) \) 的图像以及其切线,可以清晰地观察到切线斜率是如何随 \( x \) 的变化而变化的。随着 \( x \) 接近于 -1 或 1,切线斜率趋于无限,会导致导数的值迅速上升。
应用实例
了解了 \( \arcsin(x) \) 的导数后,我们可以进一步探讨其实际应用。例如,在物理学中,反正弦函数常用于描述波动现象,求导速度的变化规律,可以帮助我们分析机械系统的运动轨迹。同样在工程学中,利用反三角函数辅助构造某些特定结构的角度,也是非常常见的应用场景。
总结
本文详细探讨了反正弦函数 \( \arcsin(x) \) 的求导过程,借助隐函数求导法,我们推导出其导数为 \( \frac{1}{\sqrt{1 - x^2}} \)。从几何和应用的角度,深入理解了导数的意义和价值。随着学习的深入,掌握反三角函数的性质将为解决更复杂的数学问题奠定坚实的基础。
云作文原创内容,未经允许不得转载。