在微积分的领域中,函数的可微性与连续性常常是我们研究的重点。简单而言,一个函数如果在某一点是可微的,那么它在该点必定是连续的。然而,反过来却不一定成立:一个函数在某点连续并不意味着它在该点可微。下面,我们将从三个方面详细探讨这个问题。
一、可微的定义与性质
我们需要明确“可微”的概念。一个函数 \( f(x) \) 在某一点 \( x=a \) 可微,意味着存在极限:
\[
f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}
\]
如果这个极限存在,我们就称 \( f(x) \) 在 \( x=a \) 可微。可微性意味着函数在该点有一个确定的切线斜率,也就是说,函数在该点的行为相对光滑,没有剧烈的波动。
可微性还有一些重要的性质,比如:
1. 局部线性:在可微的点附近,函数的变化可以近似为线性的。这是通过导数来描述的。
2. 连续性:已知可微的函数在可微点是连续的。这是因为如果 \( f \) 在 \( x=a \) 可微,则我们有:
\[
\lim_{h \to 0} f(a + h) = f(a)
\]
因此,导数的存在保证了在该点的连续性。
二、连续的定义与性质
接下来,我们来看“连续”的定义。函数 \( f(x) \) 在 \( x=a \) 连续,意味着满足以下条件:
1. \( f(a) \) 是定义良好的;
2. \(\lim_{x \to a} f(x) \) 存在;
3. \(\lim_{x \to a} f(x) = f(a) \)
即在某一点的连续性要求函数的值与该点的极限相等。值得注意的是,连续性并不要求函数在该点必须光滑或有明确的方向变化。
一些常见的连续函数包括多项式函数和指数函数等。这些函数在整个定义域内都表现出良好的连续性。然而,这并不代表它们在某点的导数是存在的。
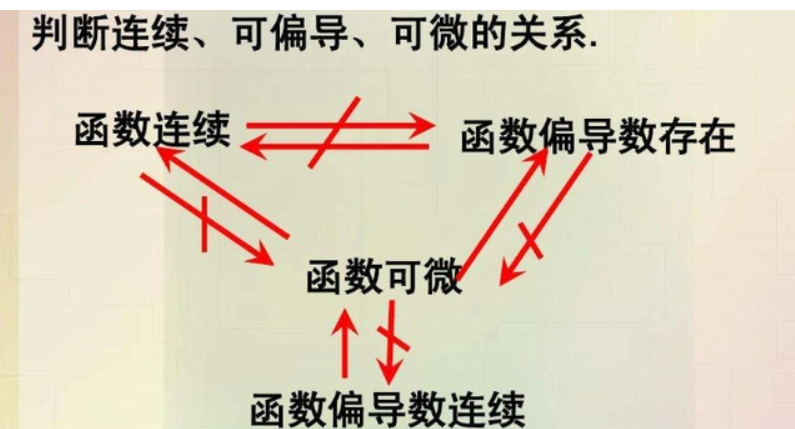
三、可微与连续的关系
了解了可微性和连续性的定义后,我们可以再深入探讨它们之间的关系。我们已经知道可微函数必然连续,但反之则未必。
例如,考虑以下简单示例,
- 绝对值函数 \( f(x) = |x| \)。
在 \( x = 0 \) 点,\( f(x) \) 是连续的,因为:
\[
\lim_{x \to 0} |x| = 0 = f(0)
\]
然而,\( f(x) \) 在 \( x=0 \) 不可微,因为左导数和右导数不相等:
\[
f'(0^-) = -1, \quad f'(0^+) = 1
\]
因此,虽然 \( f(x) \) 在 \( x=0 \) 连续,却在该点不可微。这个例子清楚地展示了连续性与可微性之间的区别。
我们还可以构造其他类似的反例。例如,分段函数、尖角函数等,尽管在某个点连续,但由于某种不规则性或不光滑性,它们在该点无法定义导数。
总结
总结:我们可以得出结论:可微的函数在该点一定连续,但连续的函数在该点不一定可微。理解这一点对我们进一步学习微积分和分析学中的更复杂主题至关重要。持续探讨可微性和连续性可以帮助我们更深入地理解函数的行为,从而在数学及其应用中做出更准确的判断。在实际应用中,理解这两者的差异尤其重要,因为很多实际问题涉及到估算函数的变化和规律,找到合适的工具来分析这些特性是非常必要的。希望本文能对大家理解这一基本概念有所帮助。
云作文原创内容,未经允许不得转载。