在数学的领域中,许多函数和概念被应用于各种科学与工程问题中。特别是三角函数,它们在解析几何、物理和工程中扮演着重要角色。而反正切函数(arctan)作为三角函数的逆函数之一,同样具有广泛的应用。本文将深入探讨arctan的定义、性质及其应用,帮助读者更好地理解这一重要的数学工具。
一:arctan的定义
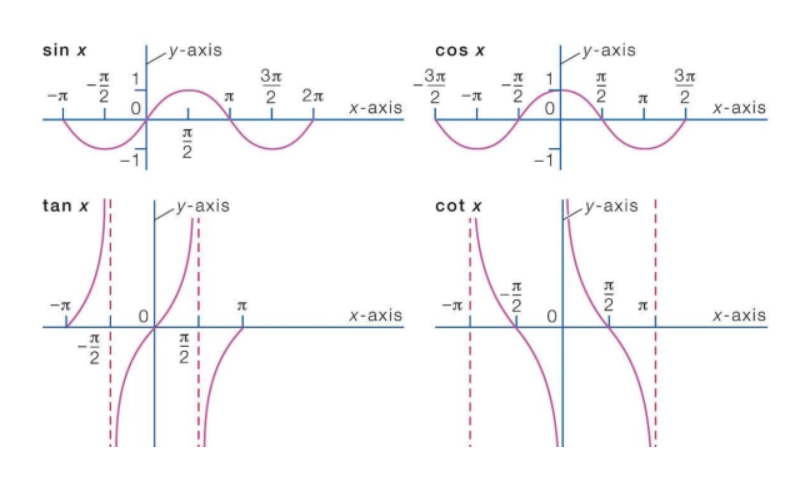
反正切函数,通常表示为arctan(x)或tan?1(x),是切函数(tan)的反函数。在给定实数x时,arctan(x)的值是一个角θ,使得tan(θ) = x。这个角θ的取值范围通常设定在(-π/2, π/2),即第一象限和第四象限。为什么要限制这个范围呢?主要是为了确保反函数的唯一性。如果不加限制,tan函数在每个周期内都有无穷多个解,因此我们必须通过限制角度范围来取得唯一的反函数值。
在直角三角形中,arctan的几何意义可以简单理解为:在一条水平基线(x轴)与某个角の(θ)边界形成的角度,直角三角形的对边与邻边的比值等于x。这一比值即为切值,而arctan则帮助我们从该切值找到相应的角度。
二:arctan的性质
arctan函数有一些值得注意的数学性质,使其在计算和分析中非常有用:
1. 单调性:arctan(x)是一个严格单调递增的函数。这意味着如果x1 < x2,则arctan(x1) < arctan(x2)。这一性质保证了arctan的可逆性,有助于解决许多方程。
2. 极限:当x趋向于无穷大时,arctan(x)趋近于π/2;而当x趋向于负无穷时,arctan(x)则趋近于-π/2。因此,arctan的值始终保持在(-π/2, π/2)的范围内。
3. 导数:arctan的导数可以通过微分法则得到:d(arctan(x))/dx = 1/(1+x2)。这一导数的形式常用于计算斜率或寻找最值问题。
4. 和差公式:arctan还有一些有趣的和差公式,例如:
- arctan(a) + arctan(b) = arctan((a + b)/(1 - ab)),条件是ab < 1。
- arctan(a) - arctan(b) = arctan((a - b)/(1 + ab)),同样有条件。
这些性质使得arctan在求解更加复杂的数学问题时非常便利。
三:arctan的应用
arctan的应用广泛,尤其是在以下几个方面:
1. 几何与三角学:在解析几何中,arctan常用于计算两点之间的夹角,特别是在计算与水平线的夹角时。通过确定两点的坐标x1, y1与x2, y2,可以直接利用arctan((y2-y1)/(x2-x1))来获得夹角。
2. 物理与工程:arctan在力学、电子学、信号处理等领域都有应用。例如,在电路分析中,通过arctan函数来计算相量的相位差,帮助描述电流和电压之间的关系。
3. 计算机图形学:在计算机绘图中,arctan常被用于确定物体在二维平面中的旋转角度。通过将对象的位置转换为极坐标,arctan能够有效地获取所需的旋转信息。
结论
总结:arctan作为反正切函数,是数学中一个极为重要的工具。通过理解其定义、性质和应用,我们不仅能够更好地掌握这一函数,还能在实践中灵活运用它解决相关问题。无论是在学术研究还是工程实践中,arctan都为我们的分析和计算提供了极大的便利。因此,深入学习和掌握arctan的相关知识,将为我们今后的学习和工作打下良好的基础。
云作文原创内容,未经允许不得转载。