平行线是几何学中重要的概念之一,它们在我们生活中无处不在。本文将探讨两条平行线之间的最短距离,以及该距离的计算方法。
_____________________________________________________________
1. 什么是平行线
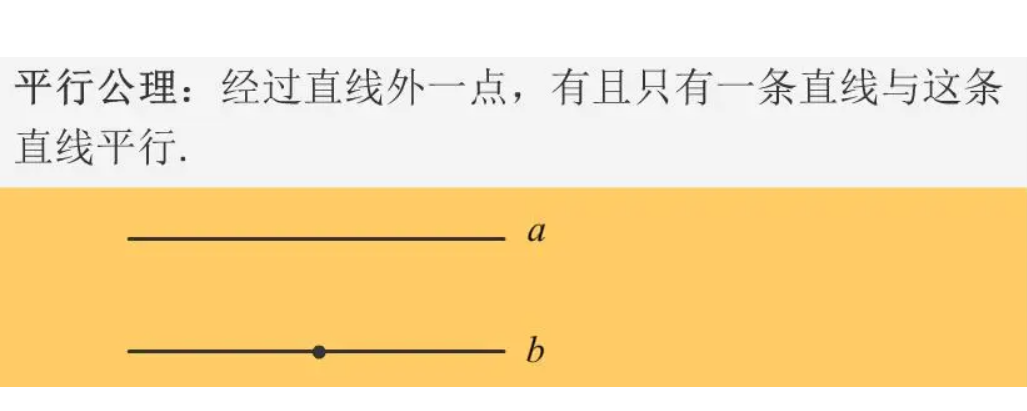
平行线是指在同一个平面上不相交的两条直线,它们具有相同的斜率,且始终保持着相同的间距。平行线有着重要的几何性质,在我们的日常生活中也有广泛的应用,例如在建筑设计、纺织品制造和航海导航等领域中。
2. 平行线之间的最短距离
当我们提到两条平行线之间的最短距离时,我们实际上是在描述两条平行线之间的垂直距离。垂直距离是从一条线到另一条线的垂直连线的长度。
3. 最短距离的计算方法
要计算两条平行线之间的最短距离,我们可以使用数学中的垂直距离公式。假设我们有两条平行线L1和L2,且已知两条线上的点A和B。
(a) 我们需要确定两条平行线上的垂直连线。我们可以通过在L1上到一个点A和在L2上到一个点B来实现。这两个点的连线将垂直于两条平行线。
(b) 然后,我们可以使用勾股定理来计算垂直连线的长度。根据勾股定理,垂直连线的长度等于两条直线的斜率之差的绝对值除以两条直线斜率之间的差的绝对值的倒数。
(c) 最后,我们可以得到两条平行线之间的最短距离。
4. 示例和应用
为了更好地理解两条平行线之间的最短距离,让我们来看一个实际的示例。假设我们有两条平行线,分别由方程y = 2x + 1和y = 2x + 5确定。
(a) 我们可以选择点A(0, 1)在第一条线上,点B(0, 5)在第二条线上。
(b) 接下来,我们可以计算垂直连线的长度。根据勾股定理,垂直连线的长度为|1 - 5| / √(2^2 + 1^2) = 4 / √5。
(c) 因此,这两条平行线之间的最短距离为4 / √5。
这种计算方法不仅仅适用于两条直线之间的最短距离,还可以扩展到曲线和曲面之间的最短距离的计算中。通过使用数学中的垂直距离公式,我们可以在实际问题中应用这一概念,例如在工程设计中优化布局或计算路径的最短距离等。
总结:
平行线之间的最短距离是两条平行线之间的垂直连线的长度。我们可以使用勾股定理来计算这个距离,该定理基于两条平行线的斜率之差和斜率之差的倒数。这个概念不仅在数学中有重要的应用,也在我们的日常生活和实际问题中起到了重要的作用。通过理解和运用这一概念,我们可以更好地理解平行线的性质,并在实践中将其运用到各种场景中。
云作文原创内容,未经允许不得转载。