方向导数和梯度grad是数学中用来描述多元函数在某一点上的变化率和方向的重要概念,它们在微分方程、最优化问题等领域具有广泛应用。本文将分别介绍方向导数和梯度grad的计算公式。
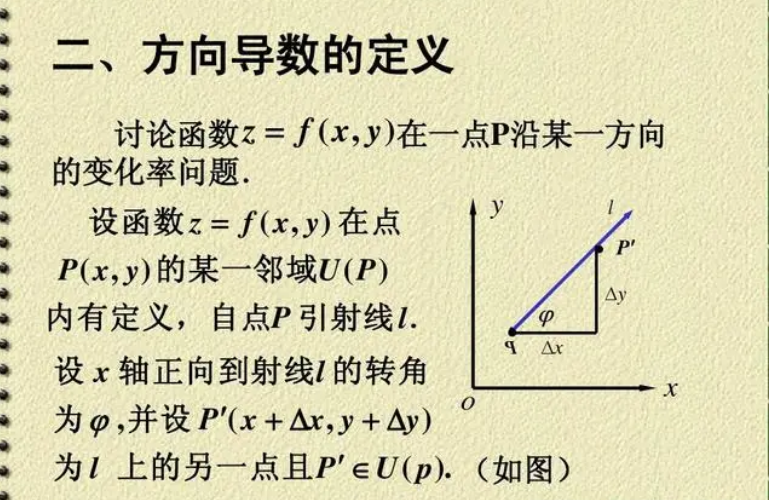
1. 方向导数的定义及计算公式
方向导数是多元函数在某一点上沿着某个方向的变化率,用来描述函数在该方向上的变化速度。对于二元函数f(x, y),在点P(x0, y0)处,沿着向量u = (a, b)的方向导数的计算公式为:
Duf(x0, y0) = ?f/?x * a + ?f/?y * b
其中?f/?x和?f/?y分别表示函数f对x和y的偏导数。
2. 梯度grad的定义及计算公式
梯度grad是一个向量,它的方向与函数在该点变化最快的方向一致,其模表示函数在该点变化的速率。对于多元函数f(x1, x2, ..., xn),在点P(x1, x2, ..., xn)处的梯度grad的计算公式为:
grad f = (?f/?x1, ?f/?x2, ..., ?f/?xn)
其中?f/?x1, ?f/?x2, ..., ?f/?xn表示函数f对每个变量x1, x2, ..., xn的偏导数。
3. 方向导数与梯度grad之间的关系
方向导数和梯度grad之间有着密切的联系。当函数f在某点处可微分时(即偏导数存在且连续),沿着梯度grad的方向导数达到最大值,且最大值等于grad f与单位向量u的点积。
具体计算方式为:
Duf(x0, y0) = |grad f(x0, y0)| * cosθ
其中,θ是梯度grad f(x0, y0)与单位向量u = (a, b)的夹角。
4. 举例说明
举例来说明方向导数和梯度grad的计算公式的应用。考虑函数f(x, y) = x^2 + y^2,求该函数在点P(1, 2)处沿着向量u = (3, 4)的方向导数。
计算函数f对x和y的偏导数:
?f/?x = 2x
?f/?y = 2y
然后,计算梯度grad f(x, y):
grad f = (2x, 2y)
最后,代入点P(1, 2)和向量u = (3, 4)计算方向导数:
Duf(1, 2) = (2x * 3) + (2y * 4) = 2*1*3 + 2*2*4 = 22
因此,函数f在点P(1, 2)处沿着向量u = (3, 4)的方向导数为22。
结语:
方向导数和梯度grad是多元函数中重要的数学概念,可以描述函数在某一点上的变化率和方向。方向导数的计算公式是基于偏导数的定义,而梯度grad则是对函数各个偏导数组合成的向量。它们之间有着密切的联系,方向导数等于梯度grad与单位向量的点积。这些概念在微分方程、最优化问题等领域有着广泛的应用。
云作文原创内容,未经允许不得转载。