在微积分中,无穷小是研究极限的重要概念之一。同阶无穷小和等价无穷小是无穷小的两个重要分类。本文将从定义、性质和应用三个方面论述同阶无穷小和等价无穷小的概念及其关系。
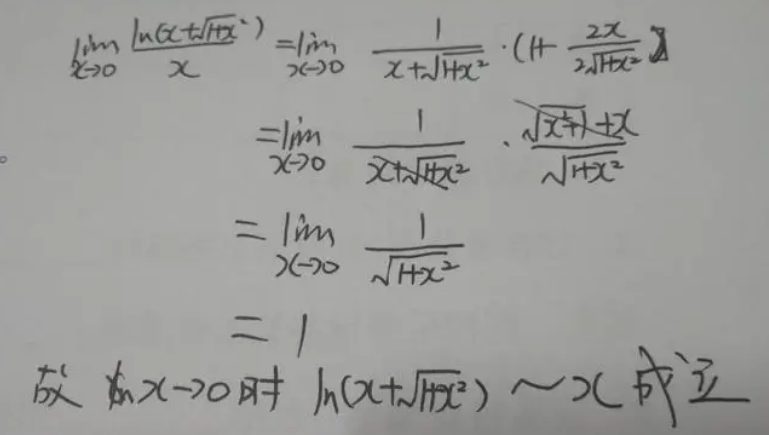
一、同阶无穷小的定义:
同阶无穷小是指在极限过程中,两个无穷小量的差趋于0。设f(x)和g(x)是定义域为区间I上的两个函数,当x趋于某个数a时,如果有lim?[f(x)-g(x)]=0,则称f(x)和g(x)是同阶无穷小。
二、等价无穷小的定义:
等价无穷小是指在极限过程中,两个无穷小量的比的极限为1。设f(x)和g(x)是定义域为区间I上的两个函数,当x趋于某个数a时,如果有lim?(f(x)/g(x))=1,则称f(x)和g(x)是等价无穷小。
三、同阶无穷小与等价无穷小的关系:
1. 同阶无穷小是等价无穷小的充分条件,即如果f(x)和g(x)是同阶无穷小,则f(x)和g(x)是等价无穷小。
证明:由同阶无穷小的定义可知,lim?[f(x)-g(x)]=0,进一步可得lim?[f(x)/g(x)-1]=0,即lim?(f(x)/g(x))=1。
2. 等价无穷小不一定是同阶无穷小。举个例子来说明:设f(x)=sin(x)和g(x)=x,当x趋于0时,lim?[f(x)/g(x)]=lim?(sin(x)/x)=1,所以f(x)和g(x)是等价无穷小。但当x趋于π时,lim?[f(x)-g(x)]=lim?(sin(x)-x)=π-π=0,即f(x)和g(x)是同阶无穷小。
3. 同阶无穷小和等价无穷小在极限计算中的应用:
在极限计算中,可以将一个函数替换为与之等价的函数,简化计算过程。同阶无穷小和等价无穷小可以作为这种替换的基础。
举个例子来说明:设f(x)=x^2和g(x)=x^2+1,当x趋于0时,lim?[f(x)/g(x)]=(x^2)/(x^2+1)=1/(1+1/x^2)。当x趋于无穷大时,lim?[f(x)/g(x)]=lim?(x^2/(x^2+1))=1。所以f(x)和g(x)是等价无穷小。
进一步地,我们可以计算lim?(f(x)/g(x))=lim?[(x^2)/(x^2+1)]=(x^2)/(x^2+1)等于1。
总结:
同阶无穷小和等价无穷小是微积分中对无穷小进行分类的重要概念。同阶无穷小指的是差趋于0的两个无穷小量,而等价无穷小指的是比趋于1的两个无穷小量。同阶无穷小是等价无穷小的充分条件,但不是必要条件。在极限计算中,我们可以利用同阶无穷小和等价无穷小来简化计算过程,提高计算效率。对于更深入的研究,我们可以进一步了解和应用这两个概念来解决更复杂的问题。
云作文原创内容,未经允许不得转载。