梯形是一种四边形,其两边平行且不等长。在梯形中,中位线定理是一个重要的几何定理,它指出梯形的两条对角线中位线的长度相等。下面将详细证明这一定理。
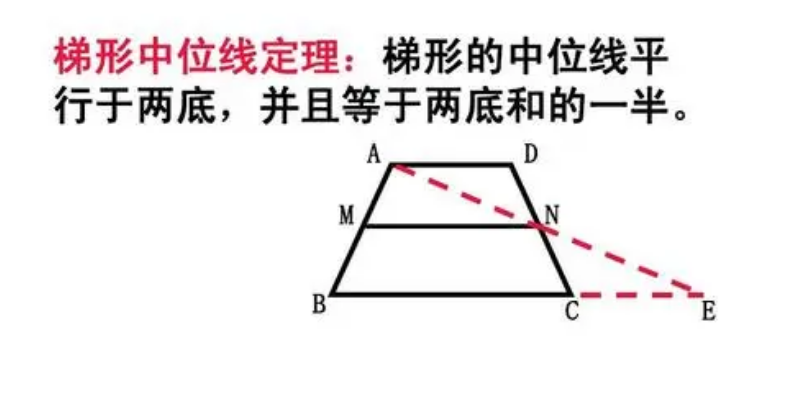
一、证明梯形的两条中位线的存在性:考虑一个梯形ABCD,其中AB和CD是梯形的平行边。我们需要证明AC和BD的中位线存在。
1.连接AD和BC,设中点分别为E和F。因为AB和CD是平行的,所以∠ADE=∠CBF,∠CAF=∠DBE。因此,三角形ADE和CBF是全等的。根据全等三角形的性质,我们可以得出AE=CF和DE=BF。
再次,连接AC和BD,设中点分别为G和H。根据平行线的性质,我们知道AE和BF平行,所以∠玩法E和∠DHG是对应角,它们相等。同样地,∠AEG和∠DHG是对应角,它们也相等。因此,三角形玩法E和DGH是全等的。根据全等三角形的性质,我们可以得出AG=DH和AE=GF。
因此,我们得出结论:在梯形ABCD中,AC的中位线EG和BD的中位线FH存在,并且EG=HF。
二、证明梯形的两条中位线相等:假设ABCD是一个梯形,其中AC的中位线为EG,而BD的中位线为FH。我们需要证明EG=HF。
由第一步的证明可知,AE=CF和AG=DH。又因为AE=GF,所以AF=GE。同理,我们可以得到DH=HF。
因此,我们得出结论:在梯形ABCD中,AC的中位线EG和BD的中位线FH相等。
三、证明梯形两条中位线的长度相等:假设ABCD和A'B'C'D'是两个梯形,AC和A'C'是两个梯形的平行边,而EG和E'G'是它们的中位线。我们需要证明EG=E'G'。
1.连接AD和A'D',设中点分别为E和E'。同样地,我们连接BC和B'C',设中点分别为F和F'。
由于AB和CD平行,所以∠ADE=∠CBF,∠A'D'E'=∠C'B'F'。因此,三角形ADE和CBF'是全等的。根据全等三角形的性质,我们可以得出AE=E'F'和DE=BF'。
同理,我们可以得到AE'=F'G和DE'=BF。因此,我们得出结论:在梯形ABCD和A'B'C'D'中,AC的中位线EG和A'C'的中位线E'G'相等。
四、总结:从以上的证明过程可以得出结论:在梯形中,两条对角线的中位线长度相等,即AC的中位线EG和BD的中位线FH相等。这一结论被称为梯形的中位线定理。通过推导和证明,我们证明了中位线的存在性、相等性和长度相等性。
梯形的中位线定理是几何学中的重要定理,具有重要的应用价值。它不仅可以被应用于梯形的性质研究和问题解决,还可以进一步推广到其他几何形状的研究中。因此,掌握这一定理对于几何学的学习和应用具有重要意义。
云作文原创内容,未经允许不得转载。